对于自然界极其缓慢的流变现象的认识和理解始终充满着奥秘，也具有重要的基础和应用研究价值。大到地壳板块的运动，小到微观原子排列无序的非晶态材料，都发生着缓慢的流动，虽然很难被我们感知。通过长达亿万年的地质缓慢流动形成我们赖以生存的稳定的地壳环境。这类极其缓慢的流变直接关系到重大工程的安全及地质灾害机理的认识和防治。 非晶态材料，比如玻璃，通常由液体的快速冷却形成，其结构类似于液体，保持着长程无序排列，在常规的时间尺度下表现为固体。但是非晶固体内部也发生着缓慢的流变行为。 中世纪教堂的古老窗户玻璃总是下部比上部厚，就是由玻璃在重力作用下的流动导致的。 上百年的沥青滴漏实验证明， 非晶态沥青看上去虽是固体，但实际上是粘性极高的液体，它在室温环境下流动极为缓慢。

　　原子（或分子）的运动行为对于认识非晶态物质的凝聚状态至关重要，也是指导如何改善非晶材料性能， 特别是力学性能的基础。在过冷液体中，很短时间内的局域原子重排 （β 驰豫）与更缓慢的原子集团运动（α 驰豫）之间随着温度的降低发生脱耦，这种驰豫模式的脱耦的发现对于理解过冷液体，以及随后的玻璃化转变和形成的玻璃材料的形变行为至关重要。而在玻璃态，驰豫极为缓慢（时间尺度从小时到年的量级），这样大的时间尺度， 在实验室里研究起来也非常困难。

　　最近，中国科学院物理研究所/北京凝聚态物理国家实验室（筹）汪卫华研究组（EX4组）博士生罗鹏在汪卫华研究员、闻平副研究员和白海洋研究员的指导下，以非晶合金（又称金属玻璃）为模型体系，在非常宽的温度和时间尺度范围，通过测量在恒定应变下材料的实时力学响应，来有效探测其缓慢的流动行为。实验表明，在较高温度下，应力响应函数单调平滑地衰减。但是随着温度降低，在实验开始30分钟左右，逐渐出现一个肩膀，而且随着温度进一步降低变得越来越明显，表现出两阶段驰豫行为（图1）。通过叠加的扩展指数函数对驰豫行为进行拟合得到特征速率和指数（图2），可以看到，在低于玻璃转变温度的某处，发生明显的驰豫模式脱耦，较快的模式表现出很弱的温度依赖，激活能只有不到0.1 eV，而且驰豫指数随着温度降低逐渐增加并最终稳定在1.3~1.5。慢驰豫模式强烈依赖于温度，激活能约为52 k_BT_g，驰豫指数随着温度降低逐渐降低。随着样品退火老化，驰豫函数明显变化，慢驰豫模式特征速率随着样品老化显著降低，而快驰豫模式不受老化影响（图3a）。驰豫过程的特征参数不依赖于施加的应变，即使超过屈服点（图3b）也如此。

　　玻璃材料处于无序和非平衡状态，必然存在原子尺度的内应力。以上结果表明，玻璃态的驰豫过程分为两步：首先发生快驰豫模式，对应于原子尺度内应力驱动的类弹道运动，此时系统被限制在势能阱中；随后体系越过能量势垒，发生更大尺度下动力学不均匀的原子重排。这一新的动力学模式脱耦的发现，拓展了我们对玻璃驰豫的传统认知，进一步完善了从动力学角度对液体到玻璃态的凝聚过程的理解（如图4）：高温液体的流动经历两个过程，即原子（或分子）在由其相邻原子（或分子）构成的笼子中振动以及随后逃离发生长程扩散；过冷液体出现新的驰豫模式脱耦，即次级势能阱之间可逆的局域重排事件（β 驰豫）和越过势能阱发生的不可逆原子集团运动（α 驰豫）；玻璃态驰豫极为缓慢，这恰恰使得局部内应力释放导致的类弹道运动与随后缓慢的原子重排不再耦合，从而观察到脱耦的动力学模式。

　　该结果表明，缓慢流动也并不简单，存在着远比我们想象丰富的内禀特性，只不过这些现象被其长时间尺度所隐藏而难以发现。

　　这项研究结果最近发表在 Physical Review Letters 118, 225901 (2017)上,并被选为编辑推荐文章。美国物理学会“Physics”网站上发表了意大利比萨大学Simone Capaccioli教授和罗马大学Giancarlo Ruocco教授写的一篇题为“Relaxation is a Two-Step Process for Metallic Glasses”的点评（Viewpoint）”文章，对这项工作做了详细的介绍和评论[30 May 2017 Physics 10, 58 https://physics.aps.org/articles/v10/58]，他们认为这种两步驰豫现象的发现促进了非晶驰豫和老化之间关系这一凝聚态物理难题的解决，不但能帮助我们更加全面地理解知之甚少的非平衡玻璃态动力学问题，而且有助于设计具有丰富功能特性和高稳定性的玻璃材料。

　　上述研究工作得到国家自然科学基金项目（51571209，51461165101）、973项目（2015CB856800）和中科院前沿科学关键研究项目（QYZDY-SSW-JSC017）的支持。

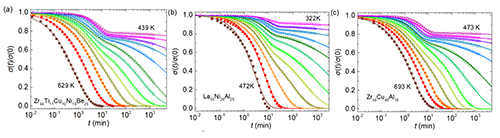图1. 三种金属玻璃体系在不同温度下的应力弛豫函数，施加的拉伸应变为0.3%。

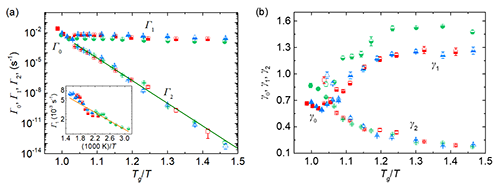图2. 拟合得到的弛豫速率（a）和指数（b）。

图3. 不同退火时间（a）和施加应变（b）下的应力弛豫函数。

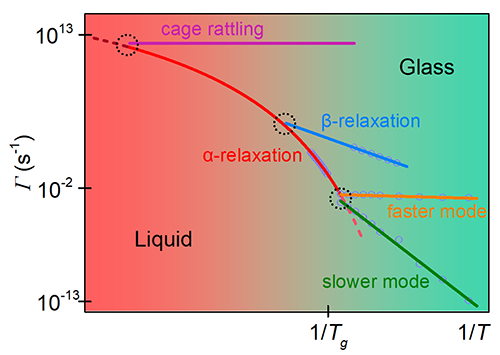图4. 从高温液体到玻璃态凝聚过程的动力学模式Arrhenius图。