中国科学院物理研究所
北京凝聚态物理国家研究中心
SM6组供稿
第37期
2017年08月18日
细菌叶绿素分子激发态多振动模耦合量子相干态的飞秒时间分辨二维电子光谱测量
玻尔曾经说过,谁要是说他懂了量子理论,那么说明他完全不了解量子力学(If you think you can talk about quantum theory without feeling dizzy, you haven't understood the first thing about it)。可见量子相干态的实验操控不是一件容易的事。 本文试图对分子激发态电子态-振动态耦合相干过程飞秒时间分辨二维电子光谱测量给出一个直观的物理图像,用于诠释最近在这方面取得的相关研究进展:Coupling of multi-vibrational modes in bacteriochlorophyll a in solution observed with 2D electronic spectroscopy,Chemical Physics Letters 683 (2017) 591–597。
量子相干态传能是一种新的高效传能机制,首先在光合作用原初传能过程中由飞秒时间分辨二维电子光谱的实验获得证实。不同于传统的Fröster能量由高到低的点对点传能机制,量子相干态传能具有波函数叠加并高度离域及激发能共享的特性,从而避开了能量由高到低、空间距离由近及远的顺序传能的约束。
然而用于量子相干态测量的二维电子光谱的原理和实验并不直接明了。在量子相干态的测量过程中,存在两个难以逾越的限制。一个是不确定性原理,另一个是量子相干叠加态的测量。前者指出无法同时准确测定一对共轭的物理量,如能量和时间;动量与位置。而量子态的线性叠加原理表明,对于任何一个量子相干叠加态的测量,其结果都会坍缩到某个本征态。而对于电子激发态上形成的量子相干态,对其测量过程将同时受到上述原理的双重限制。这是由于电子相干态的寿命短,要求极高的时间分辨率,以激光测量为例,须用飞秒量级的脉冲激光,导致很宽的频谱,从而无法同时实现能量(光谱)与时间(退相干时间)的同时精密测量;另一方面当电子相干态受到测量过程的扰动时就坍缩到某个本征态,从而无法获得叠加态的信息。尽管飞秒激光的出现,使得制备分子电子态的相干叠加态变得相对容易,然而对于实现相干叠加态测量方法的探索则颇费一番周折,原因是任何一个可靠的实验方法必须绕开上述两大限制。
二维光谱所测量的系统是由大量分子构成的系综,由于被测系综的不均匀性,任何光学信息的提取都将以光子回波的形式获取。 光子回波借鉴了核磁共振技术中的核自旋回波的概念:核自旋在一π/2磁脉冲激励后,在间隔时间τ用一个π脉冲激发,系统再经历一个τ时间后就会形成一个回波信号。该过程可以用Bloch 方程描述。类似的,二维电子光谱测量的也是光学回波信号,二维电子光谱本质上为非线性光谱,是三光子回波的四波混频过程。其测定的是系统在受激发脉冲微扰后的极化辐射电场。 对于双光子回波过程,其本质也是三光子回波,只是将三光子回波中的第二和第三个脉冲间的延时设为零(二阶极化张量为零)。
电场与分子能级跃迁的相互作用随时间的演化过程可由含时密度矩阵的微扰理论进行展开。对于简单的二能级系统(四个密度矩阵元:\(\rho _{00},\rho _{01},\rho _{10},\rho _{11}\)),密度矩阵的演化数学形式可用光学Bloch方程( \(\frac{ds(t)}{dt}=\Omega (t)\times S(t)\))描述:外加电场的作用如同加在三维矢量(\(S(t)\))上的旋转矩(\(\Omega(t)\)),\(S_{z}=\rho _{00}-\rho _{11}\),\(S_{x}=\rho _{10}+\rho _{01}\),\(S_{y}=\rho _{10}-\rho _{01}\)。其中Sz表示能级布局数随时间的演化,而Sx和Sy则表示相干态的演化。 图1a给出了更为直观的光子回波形成过程的Bloch矢量表示(双光子回波作为简并三光子回波的特例);图1b给出了三光子回波的脉冲序列及回波信号出现在时间轴的位置,回波信号的测量是电场的测量而非光强的测量,这样保持了回波电场的位相信息,实验中采用一脉冲光作为本机振荡信号与回波信号进行干涉形成超外差测量。同时图1b 还揭示了如何在一个被测系统中利用第一个脉冲写入一个相干态,然后通过第三个脉冲读出一个相干态的过程。图1c 给出了二能级系统在三个时间序列脉冲电场作用下密度矩阵元的演化,显然第一个脉冲激发了一个相干态ρ01,第二个脉冲的作用获得了激发态的布居ρ11,第三个脉冲同样得到的是相干态ρ10,第三个脉冲类似于π脉冲,所得到的相干态ρ10经时间τ=t1=t3 后形成回波电场而被探测到。可见ρ10是ρ01的共轭量,即时间上的反演关系。可见回波信号可以真实地反映相干态的激发电场。可见读出的相干态是一个电场信息,要获得光谱信息必须在时域内对电场进行傅里叶变换。原则上通过扫描第一和第二个脉冲之间的延时,获得回波电场随扫描时间的演化,再对其进行傅里叶变化就能够获得进傅里叶变换重构而成的相干激发的光谱。回波信号中可以获得两个信息,一是回波电场的光谱,另外是通过重构而成的相干激发光谱,其数学关系可以表达如下:
\(S^{(3)}(\omega _{1},T,\omega _{3})\propto \int_{0}^{\infty }\int_{0}^{\infty }S^{(3)}(t _{1},T,t_{3})e^{m\omega _{1}t_{1}}e^{+\omega _{3}t_{3}}dt_{3}dt_{1}\)
S(3)(t3,T,t1)为宏观三阶极化场的含时演化,S(3)(ω1,T,ω3)为由此构建的某一布居时间T处的二维光谱S(3)(ω1,ω3)。
在相当长的时间内,实验上对上述双重傅里叶变换无从下手,直到意识到对回波信号直接进行光谱测量就相当于在硬件上进行一次对t3的傅里叶变化,给问题就变成一维傅里叶变换,使得上述问题迎刃而解。上式也表明,所有的测量都是在时域内实现的,激发态布居数变化可以通过对等待时间T进行高精度延时而实现高时间分辨,同时通过扩展t3的扫描范围来实现光谱(能量)的高分辨测量。二维电子光谱就是通过这种在双时域中的非同时性测量,绕开了不确定性原理的限制。
对于简单的二能级系统而言,基于三光子回波测量的二维电子光谱仅仅能够获得相干激发的信息,也就是说回波电场信号对应的光谱和重构的相干激发光谱是等价的。对于多能级及其他复杂系统,相干态的产生除了光场相干激发外,还可以通过能量转移等其他途径来实现,导致写入的相干电场不同于读出的回波光场,从而可以确定相干激发光谱和回波探测光谱间的相关性,由此可推断相干态的演化路径。除了确定相干激发和回波探测光谱的相关性外,二维光谱的另一突出优点是量子拍频的产生和测量。 在形成布居数的密度矩阵中,如果相同电子态的左矢和右矢相差一个振动能级或电子态耦合劈裂的能级差,那么回波信号就会在布局延时时间(等待时间)T轴上形成和该振动周期或电子态耦合劈裂相对应的量子拍,给出相干态振动或电子态相干的信息。图2(a)中布具数密度矩阵的左矢和右矢(下划线部分)都处于电子态和振动态的基态(g,e分别表示电子态的基态和激发态,下标0,1则表示震动的基态和激发态),表示处于基态,不会形成量子拍。而图2(b)相应的左矢处于电子态和振动态的基态, 右矢处于电子态基态和振动态的激发态,形成一个振动量子拍。
因此在含量子拍的二维光谱中往往通过三维傅里叶变换来获取相干激发及相干态的信息。 尽管在光谱测量中只能获得各本征态能级的信息,但由于量子拍频效应的存在,能够获取系统相应本征态是否处于相干状态的信息,从而绕开了波包坍缩到本征态的限制。
由于量子拍频能够同时反映相干电子态(电子态劈裂)和振动态的信息,因此二维光谱研究领域中,如何区分电子态与振动态相干、电子态与振动态耦合相干是仍然是尚未彻底解决的科学难题。
另一方面,在处理振动态与电子态耦合的过程中,大多采用位移振子模型(displaced oscillator),即电子激发态的势能面和基态的势能面在核运动方向产生一个位移。在该模型中,采取单振动模和电子势能面耦合的方式。对于简谐振动,不同振动模式间的耦合是被禁阻的,而对于多原子分子,随着非谐性效应的加大,出现不同振动模对应的激发态势能面的交叉,并在势能面交叉区域内形成不同振动模的耦合,使得二维光谱相干态的复杂性进一步增加。
中国科学院物理研究所/北京凝聚态物理国家实验室(筹)软物质物理院重点实验室翁羽翔研究组在基金委重大仪器项目基金(项目批准号:21227003)和物理所择优经费的支持下,建立了飞秒时间分辨二维电子光谱仪(Chinese Journal of Chemical Physics,2015, 28,509-517),应用上述设备研究了细菌叶绿素分子的低振动频模与电子态耦合的相干激发,观测到了不同振动模在共振拉曼激发过程中的多个低频振动模和电子态耦合而形成的多振动模量子拍(波包),并在实验的基础上提出了二维光谱中的多振动模相干耦合的新机制,给出了多模耦合导致相干态的费曼路径及相应二维光谱所对应的范式谱,丰富了二维电子光谱研究领域的实验和理论。论文表于为纪念去年去世的诺贝尔奖获得者Zewail教授而出版的专刊上(Ahmed Zewail Commemoration Issue of Chemical Physics Letters, 2017)。第一作者为博士研究生岳帅。该项工作从理论准备到实验设备搭建和最后的数据分析经历了一个漫长的探索过程,量子相干态虽说不像先前那样捉摸不透,然而玻尔的经典名言依然适用。
量子相干态传能是一种新的高效传能机制,首先在光合作用原初传能过程中由飞秒时间分辨二维电子光谱的实验获得证实。不同于传统的Fröster能量由高到低的点对点传能机制,量子相干态传能具有波函数叠加并高度离域及激发能共享的特性,从而避开了能量由高到低、空间距离由近及远的顺序传能的约束。
然而用于量子相干态测量的二维电子光谱的原理和实验并不直接明了。在量子相干态的测量过程中,存在两个难以逾越的限制。一个是不确定性原理,另一个是量子相干叠加态的测量。前者指出无法同时准确测定一对共轭的物理量,如能量和时间;动量与位置。而量子态的线性叠加原理表明,对于任何一个量子相干叠加态的测量,其结果都会坍缩到某个本征态。而对于电子激发态上形成的量子相干态,对其测量过程将同时受到上述原理的双重限制。这是由于电子相干态的寿命短,要求极高的时间分辨率,以激光测量为例,须用飞秒量级的脉冲激光,导致很宽的频谱,从而无法同时实现能量(光谱)与时间(退相干时间)的同时精密测量;另一方面当电子相干态受到测量过程的扰动时就坍缩到某个本征态,从而无法获得叠加态的信息。尽管飞秒激光的出现,使得制备分子电子态的相干叠加态变得相对容易,然而对于实现相干叠加态测量方法的探索则颇费一番周折,原因是任何一个可靠的实验方法必须绕开上述两大限制。
二维光谱所测量的系统是由大量分子构成的系综,由于被测系综的不均匀性,任何光学信息的提取都将以光子回波的形式获取。 光子回波借鉴了核磁共振技术中的核自旋回波的概念:核自旋在一π/2磁脉冲激励后,在间隔时间τ用一个π脉冲激发,系统再经历一个τ时间后就会形成一个回波信号。该过程可以用Bloch 方程描述。类似的,二维电子光谱测量的也是光学回波信号,二维电子光谱本质上为非线性光谱,是三光子回波的四波混频过程。其测定的是系统在受激发脉冲微扰后的极化辐射电场。 对于双光子回波过程,其本质也是三光子回波,只是将三光子回波中的第二和第三个脉冲间的延时设为零(二阶极化张量为零)。
电场与分子能级跃迁的相互作用随时间的演化过程可由含时密度矩阵的微扰理论进行展开。对于简单的二能级系统(四个密度矩阵元:\(\rho _{00},\rho _{01},\rho _{10},\rho _{11}\)),密度矩阵的演化数学形式可用光学Bloch方程( \(\frac{ds(t)}{dt}=\Omega (t)\times S(t)\))描述:外加电场的作用如同加在三维矢量(\(S(t)\))上的旋转矩(\(\Omega(t)\)),\(S_{z}=\rho _{00}-\rho _{11}\),\(S_{x}=\rho _{10}+\rho _{01}\),\(S_{y}=\rho _{10}-\rho _{01}\)。其中Sz表示能级布局数随时间的演化,而Sx和Sy则表示相干态的演化。 图1a给出了更为直观的光子回波形成过程的Bloch矢量表示(双光子回波作为简并三光子回波的特例);图1b给出了三光子回波的脉冲序列及回波信号出现在时间轴的位置,回波信号的测量是电场的测量而非光强的测量,这样保持了回波电场的位相信息,实验中采用一脉冲光作为本机振荡信号与回波信号进行干涉形成超外差测量。同时图1b 还揭示了如何在一个被测系统中利用第一个脉冲写入一个相干态,然后通过第三个脉冲读出一个相干态的过程。图1c 给出了二能级系统在三个时间序列脉冲电场作用下密度矩阵元的演化,显然第一个脉冲激发了一个相干态ρ01,第二个脉冲的作用获得了激发态的布居ρ11,第三个脉冲同样得到的是相干态ρ10,第三个脉冲类似于π脉冲,所得到的相干态ρ10经时间τ=t1=t3 后形成回波电场而被探测到。可见ρ10是ρ01的共轭量,即时间上的反演关系。可见回波信号可以真实地反映相干态的激发电场。可见读出的相干态是一个电场信息,要获得光谱信息必须在时域内对电场进行傅里叶变换。原则上通过扫描第一和第二个脉冲之间的延时,获得回波电场随扫描时间的演化,再对其进行傅里叶变化就能够获得进傅里叶变换重构而成的相干激发的光谱。回波信号中可以获得两个信息,一是回波电场的光谱,另外是通过重构而成的相干激发光谱,其数学关系可以表达如下:
\(S^{(3)}(\omega _{1},T,\omega _{3})\propto \int_{0}^{\infty }\int_{0}^{\infty }S^{(3)}(t _{1},T,t_{3})e^{m\omega _{1}t_{1}}e^{+\omega _{3}t_{3}}dt_{3}dt_{1}\)
S(3)(t3,T,t1)为宏观三阶极化场的含时演化,S(3)(ω1,T,ω3)为由此构建的某一布居时间T处的二维光谱S(3)(ω1,ω3)。
在相当长的时间内,实验上对上述双重傅里叶变换无从下手,直到意识到对回波信号直接进行光谱测量就相当于在硬件上进行一次对t3的傅里叶变化,给问题就变成一维傅里叶变换,使得上述问题迎刃而解。上式也表明,所有的测量都是在时域内实现的,激发态布居数变化可以通过对等待时间T进行高精度延时而实现高时间分辨,同时通过扩展t3的扫描范围来实现光谱(能量)的高分辨测量。二维电子光谱就是通过这种在双时域中的非同时性测量,绕开了不确定性原理的限制。
 |
| 图1. 基于三光子回波测量的二维电子光谱原理示意图。(a)光学Bloch矢量所描述的双光子回波;(b)三光子回波过程的脉冲光激发时序及回波信号超外差测量示意图;第一个脉冲可表示为相干态的写入,第三个脉冲表示相干态的读出。 (c) 两能级系统三光子回波过程所对应的含时密度矩阵演化示意图。 |
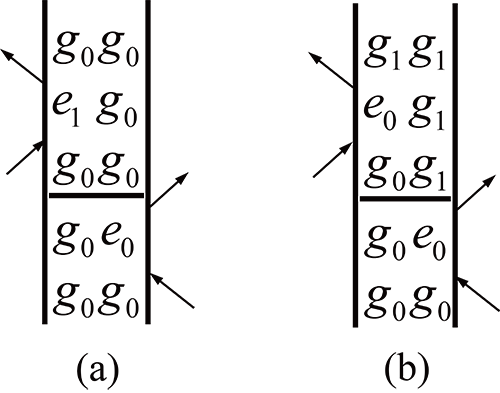 |
| 图2.三光子回波过程的典型费曼双边图。(a)系统基态布居数密度矩阵不含相干态;(b)系统基态布居数密度矩阵包含一个振动相干态。 |
由于量子拍频能够同时反映相干电子态(电子态劈裂)和振动态的信息,因此二维光谱研究领域中,如何区分电子态与振动态相干、电子态与振动态耦合相干是仍然是尚未彻底解决的科学难题。
另一方面,在处理振动态与电子态耦合的过程中,大多采用位移振子模型(displaced oscillator),即电子激发态的势能面和基态的势能面在核运动方向产生一个位移。在该模型中,采取单振动模和电子势能面耦合的方式。对于简谐振动,不同振动模式间的耦合是被禁阻的,而对于多原子分子,随着非谐性效应的加大,出现不同振动模对应的激发态势能面的交叉,并在势能面交叉区域内形成不同振动模的耦合,使得二维光谱相干态的复杂性进一步增加。
中国科学院物理研究所/北京凝聚态物理国家实验室(筹)软物质物理院重点实验室翁羽翔研究组在基金委重大仪器项目基金(项目批准号:21227003)和物理所择优经费的支持下,建立了飞秒时间分辨二维电子光谱仪(Chinese Journal of Chemical Physics,2015, 28,509-517),应用上述设备研究了细菌叶绿素分子的低振动频模与电子态耦合的相干激发,观测到了不同振动模在共振拉曼激发过程中的多个低频振动模和电子态耦合而形成的多振动模量子拍(波包),并在实验的基础上提出了二维光谱中的多振动模相干耦合的新机制,给出了多模耦合导致相干态的费曼路径及相应二维光谱所对应的范式谱,丰富了二维电子光谱研究领域的实验和理论。论文表于为纪念去年去世的诺贝尔奖获得者Zewail教授而出版的专刊上(Ahmed Zewail Commemoration Issue of Chemical Physics Letters, 2017)。第一作者为博士研究生岳帅。该项工作从理论准备到实验设备搭建和最后的数据分析经历了一个漫长的探索过程,量子相干态虽说不像先前那样捉摸不透,然而玻尔的经典名言依然适用。
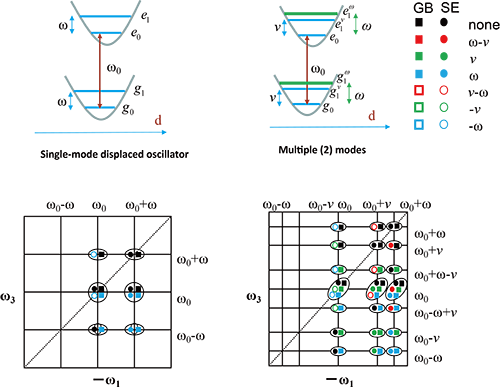 |
| 图3.单模(ω)位移谐振子模型及由相应费曼路径导出的相干振动二维电子光谱范式图(左);双模(ω,ν)位移谐振子模型及由相应费曼路径导出的相干振动二维电子光谱范式图(右);图中彩色符号对于相干路径,黑色符号对应非相干路径。ω0为电子态激发频率。GB:基态漂白;SE:受激辐射。 |

