中国科学院物理研究所
北京凝聚态物理国家研究中心
SF6组供稿
第53期
2017年11月10日
受拓扑保护的等离激元研究取得进展
在凝聚态物理当中,等离激元是最重要的元激发之一。1951年David Pines和David Bohm预测提出等离激元的概念,用于描述在固体当中由于库伦相互作用产生的电荷密度集体振荡的元激发。而后1957年,Rufus Ritchie又将等离激元的概念延伸到表面和界面上,提出了表面等离激元的存在。自此之后,科学家对于等离激元性质的研究持续了60年之久并仍在发展壮大,由此逐渐衍生出等离子体光子学这一前沿领域及其它诸多交叉应用领域。对于任何可能的应用,最为重要的问题就是等离激元的寿命。在普通材料体系中,等离激元通常只能存在于很小的动量范围,因为当它的色散进入电荷空穴连续区时,就会与转化为单粒子激发从而导致其寿命的急剧衰减。此外,一般材料中,杂质散射也是必然的另一种衰减通道。这种急剧衰减的现象几乎对于所有等离激元都是适用的,无论它是来自普通金属中具有抛物线型色散的有质量电子,还是来自于石墨烯等材料中具有线性色散的无质量狄拉克电子。对于拓扑非平庸的狄拉克电子形成的等离激元又会是怎样的呢?一个典型的例子是在三维拓扑绝缘体的表面态上,由于动量和自旋的锁定使得表面态电子免受任何非磁性杂质的背散射从而拥有更长的寿命,那么它所形成的集体模式也会具有很长的寿命吗?在拓扑绝缘体中关于等离激元的理论和实验工作如火如荼的开展,但尚无关于其长寿命方面的实验观测报导。
中国科学院物理研究所/北京凝聚态物理国家实验室(筹)表面物理国家重点实验室SF06组的郭建东研究员、朱学涛副研究员和博士生曹彦伟(已毕业)等人,在2015年成功研制了世界首台具有能量-动量二维解析能力的高分辨电子能量损失谱仪(2D-HREELS)[Rev. Sci. Instrum. 86, 083902 (2015)]。该系统将一个带有特殊设计电磁透镜组的电子束单色器与商业化的二维半球形分析器结合,可以同时探测到散射电子能量和动量的信息。该谱仪可以对表面元激发进行高分辨、高效率的测量,能够给出电子、晶格、及其集体激发的综合信息,是研究低维材料体系多体作用的强大工具。
近期,物理所表面物理国家重点实验室SF06组博士生贾逊、张书源在朱学涛副研究员、郭建东研究员的指导下,与美国路易斯安纳州立大学的张坚地教授、E. W. Plummer教授,波士顿学院的K. Kempa教授,台湾大学的周方正教授、R. Sanker研究员等合作,利用上述2D-HREELS系统,在实验上观测到了三维拓扑绝缘体Bi2Se3表面态产生的一支反常的声学支等离激元模式。他们观测并分析出这支等离激元模式的诸多特征:
相关工作链接:
http://aip.scitation.org/doi/citedby/10.1063/1.4928215
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.119.136805
中国科学院物理研究所/北京凝聚态物理国家实验室(筹)表面物理国家重点实验室SF06组的郭建东研究员、朱学涛副研究员和博士生曹彦伟(已毕业)等人,在2015年成功研制了世界首台具有能量-动量二维解析能力的高分辨电子能量损失谱仪(2D-HREELS)[Rev. Sci. Instrum. 86, 083902 (2015)]。该系统将一个带有特殊设计电磁透镜组的电子束单色器与商业化的二维半球形分析器结合,可以同时探测到散射电子能量和动量的信息。该谱仪可以对表面元激发进行高分辨、高效率的测量,能够给出电子、晶格、及其集体激发的综合信息,是研究低维材料体系多体作用的强大工具。
近期,物理所表面物理国家重点实验室SF06组博士生贾逊、张书源在朱学涛副研究员、郭建东研究员的指导下,与美国路易斯安纳州立大学的张坚地教授、E. W. Plummer教授,波士顿学院的K. Kempa教授,台湾大学的周方正教授、R. Sanker研究员等合作,利用上述2D-HREELS系统,在实验上观测到了三维拓扑绝缘体Bi2Se3表面态产生的一支反常的声学支等离激元模式。他们观测并分析出这支等离激元模式的诸多特征:
- 这支模式的色散关系在一个很大的动量范围(至少到第二布里渊区中心)呈现出几乎线性的行为,并且色散关系不依赖于晶格的周期性。通过对磁性原子Mn掺杂的Bi2Se3的对比实验,发现这支模式与狄拉克锥有同生同灭的特性。于是在实验上确认这支模式是来自狄拉克电子的声学支等离激元(图一、图二)。
- 他们发现这支模式无论是在电荷空穴连续区内或外都呈现出弱衰减的特性,而这一特性从未在其它任何体系中出现。于是推测这一特性与拓扑态的保护有关,进而说明拓扑保护不仅仅可以出现在单电子层面,对于集体模式也是适用的(图三)。
- 这支模式的能量色散比以往任何理论预测的都要低,并且与表面声子的能量类似,预示着这支等离激元和表面声子之间有着很强的相互作用(图三)。
相关工作链接:
http://aip.scitation.org/doi/citedby/10.1063/1.4928215
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.119.136805
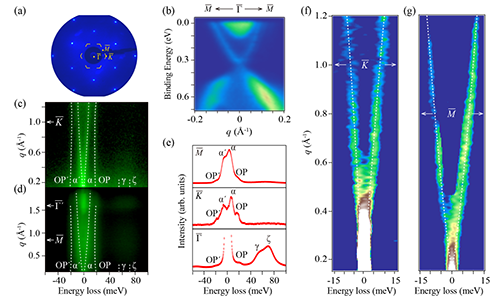 |
| 图一(a)Bi2Se3(0001)的低能电子衍射斑点。(b)Bi2Se3(0001)沿高对称方向\( \overline{\Gamma}-\overline{M}\)的能带结构。(c)和(d)分别沿\( \overline{\Gamma}-\overline{K}\)和\( \overline{\Gamma}-\overline{M}\)方向的HREELS二维图谱。(e)在高对称点\( \overline{\Gamma}\),\( \overline{K}\)和\( \overline{M}\)的EDC。(f)和(g)分别是(c)和(d)的二次微分图。 |
 |
| 图二(a)Mn-doped Bi2Se3(0001)沿 方向的HREELS二维图谱,插图为Mn-doped Bi2Se3(0001)沿高对称方向 的能带结构。(b)在高对称点 和 的EDC。(c)是(a)的二次微分图。 |
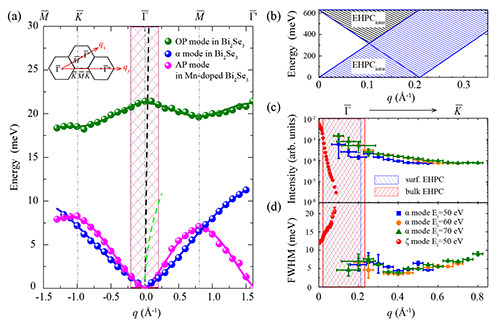 |
| 图三(a)Bi2Se3中α 模式,OP模式和Mn-doped Bi2Se3中AP 模式的色散关系。(b)无质量狄拉克电子的电荷空穴连续区。(c)和(d)分别为Bi2Se3中α模式的归一化强度与线宽。 |

