最近，中国科学院物理研究所/北京凝聚态物理国家研究中心的科研团队在拓扑物态研究领域又取得了新的成果，首次在声子体系中预言了三重简并和四重简并两类“双外尔点”，这项工作是继“拓扑绝缘体”、“量子反常霍尔效应”、“外尔费米子”、“三重简并费米子”之后在能带拓扑领域的又一理论进展，为单晶固体材料中声子拓扑态的研究开辟了新的方向。
　　近年来，拓扑能带论在电子体系和光子体系中取得了很大成就，也萌生出了许多新兴的研究方向。但声子系统中的拓扑态大多还局限于对人工体系经典声波的研究，能量尺度局限于KHz量级上。 然而参与热导、电声耦合的声子都是量子力学极限下THz量级的声子决定的。因此对于原子尺度上声子拓扑性的研究具有十分重要的意义。
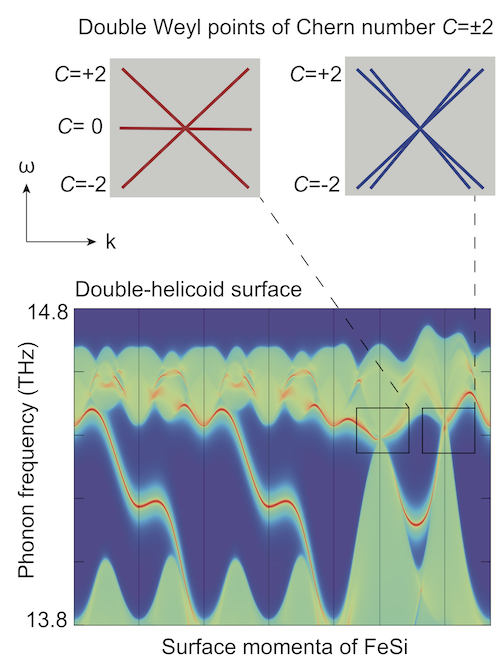
　　这个工作的第一第二作者为T03组方忠研究员的博士研究生张田田和宋志达，通讯作者为T03组的方辰特聘研究员和L01组的陆凌研究员，团队其他成员是T03组的翁红明研究员和耶鲁大学的A. Alexandradinata博士。这一研究组发现一组无中心对称过渡金属单硅化物MSi (M=Fe,Co,Mn,Re,Ru) 的声子谱中广泛存在两种“双外尔点”。第一类双外尔点是在布里渊区中心的所有三重简并点，包括连接零能的三条声学声子模式，三条能带的陈数分别为0，±2，他们称之为“Spin-1 Weyl”点。第二类双外尔点是布里渊区边界角上的四重简并点，由非简单空间群保护，两两能带的陈数分别为±2，他们称之为“Charg-2 Dirac”点。与电、光系统的外尔点性质无异，声子系统中的外尔点也有螺旋的表面态与体态的拓扑相对应的性质，因此MSi体态中的双外尔点亦会有双螺旋的表面态与之相应。MSi的双螺旋表面态同样可以用外尔斯特拉斯椭圆函数所生成的“非紧致的黎曼面”描述。因为这类预言的材料真实存在，实验结果也有望能证实这一预言。
　　这一工作作为封面文章在2018年第一期的PRL发表：Phys. Rev. Lett. 120, 016401 (2018)。该工作得到了科技部国家重点研发计划No.2016YFA0302400（方辰、陆凌），No.2016YFA0300600 (方辰、翁红明)， No.2017YFA0303800 (陆凌), 国家自然基金No.11674370（方辰），No.11421092（翁红明、方忠），No.11721404（陆凌），国家973项目No.2013CB921700（方忠），耶鲁大学博士后奖学金（A. Alexandradinata）的支持。
　　文章链接：https://doi.org/10.1103/PhysRevLett.120.016401