在传统的基于自由电子扩散的热电输运中，塞贝克系数α电子的化学势μ对外加温度梯度的微分（α≡-Δμ/ΔT），α等同于电子的熵。电子是费米子，受泡利不相容原理制约，其自由度非常有限。因此，电子的α可以用Mott公式表示：

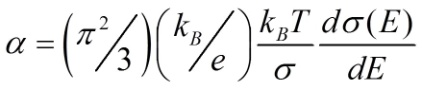
　　这里，σ(E)是电子电导率，E, σ, k_B, e分别是电子能量，电导率，玻尔兹曼常数和元电荷。在电子浓度足够高时，材料表现出较好的电导率，σ(E)几乎不随能量变化，塞贝克系数α则非常小。与费米子相反，波色子不受泡利不相容原理的限制，玻色子（其统计分布函数也由化学势和温度表示）的塞贝克系数α可表达为：

　　这里C是热容，n是粒子的密度。即波色子的α是每个粒子的比热容，不取决于粒子的数量。因此，如果可以利用热电材料的温度梯度来驱使玻色子，比如铁磁体和反铁磁体中的磁振子（热驱动的自旋进动有着和晶格相同的周期性，这种周期性的相干波被称为磁振子），然后让磁振子通过电子-电子(s-d)相互作用进一步作用于导电电子，这将产生非常规热电效应。这种相互作用正是自旋塞贝克效应和磁振子曳引效应的根源。近来，定量化的磁振子曳引效应理论在金属铁、钴、镍材料中已获得验证，该理论表明磁振子曳引产生的热电势比传统金属的热电势高出1到2个数量级。这是迄今唯一一个自旋效应热电势远大于电子效应的实例，其原因就在于熵的论据。由此，深入探究磁有序材料中传导电子与磁化强度的热涨落，即磁振子或顺磁体磁振子（para-magnons）的基本相互作用，将自旋作为一个新的自由度来打破塞贝克系数（α）和电导率的耦合关系，进而提高热电材料输运性能，是当前热电输运研究的一个热点。

　　自2017年以来，由中国科学院物理研究所/北京凝聚态物理国家研究中心赵怀周研究员、美国Ohio State University的Joseph Heremans教授、North Carolina State University的Daryoosh Vashaee教授、以及ORNL的Raphael P. Hermann博士组成的合作团队在反铁磁MnTe材料热电磁耦合输运研究方面取得重要成果，首次将上述磁曳引热电势理论延伸至磁有序之外的顺磁态MnTe，从而拓宽了可以通过自旋效应提高热电材料性能的渠道（见示意图一）。实验及理论模拟发现，与磁有序态相同，顺磁态MnTe的磁振子曳引塞贝克系数依然遵循如下关系式：

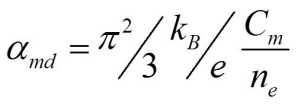
　　这里，C_m是磁振子的比热容，n_e是传导电子的密度（在金属中通常是s和p电子）。

　　研究团队在Li掺杂的Mn_1-xLi_xTe（x=0~0.06）系列材料中，首次发现磁振子曳引热电势可以延伸至高温顺磁态并达到3倍尼尔温度处（3×T_N），且曳引热电势强度随样品中载流子浓度增加而降低（图二）。磁比热容分析（图三（B）），以及经由Hall测试所得的有关样品的载流子迁移率和弛豫时间数据（图三（B），（D）），结合中子散射实验结果（图四），证实了MnTe反铁磁体中短程有序的局域磁化在高于磁性转变温度（居里温度或奈尔温度）时依然存在，并且通过对电子的曳引作用贡献额外热电势。基于以上实验结果，团队首次提出顺磁拖曳热电势理论模型：同铁磁体和反铁磁体中的磁振子一样，顺磁体中热驱动的局域磁化强度的涨落会和电子相互作用。这种涨落（我们称之为顺磁磁振子，paramagnons）会和磁振子一样对温度梯度敏感，显示出局域的磁有序和有限的寿命。由于驱动磁振子的电子-电子相互作用（s-d相互作用）探测到的是在10-13秒或更短的时间尺度下的磁结构，在这个时间尺度下，顺磁磁振子和磁振子同样可以对电子施加类似流体动力的曳引作用，从而极大地提高热电势。基于实验测量得到的磁比热容、载流子寿命和浓度，以及顺磁磁振子的寿命和自旋空间关联长度等参数（图四（F）），计算拟合得到理论热电势与实验测量数据完全吻合（图二），证实了顺磁拖曳热电势理论模型的正确性。

　　这项成果首次在高温磁性半导体热电材料中发现并确认顺磁拖曳热电势效应，丰富了人们对于磁热电耦合输运理论的认识，对发现新型磁热电材料有重要启发意义。相关论文近日发表于Science开源子刊Science Advances, 文章链接DOI:10.1126/sciadv.aat9461

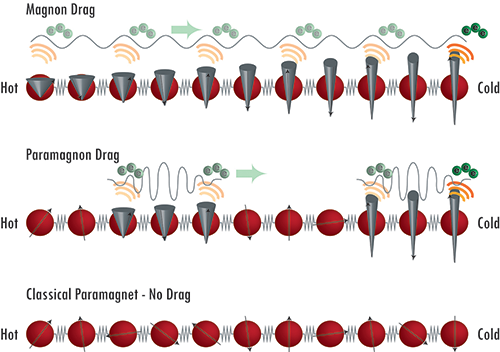图一：磁振子是单个原子自旋热涨落产生的格波，它可沿热梯度方向对导电电子产生曳引作用，从而对热电势作出贡献；而在顺磁态下，局域化的热涨落则形成小的磁振子波包，同样贡献热电势；传统的顺磁体则不产生曳引热电势。

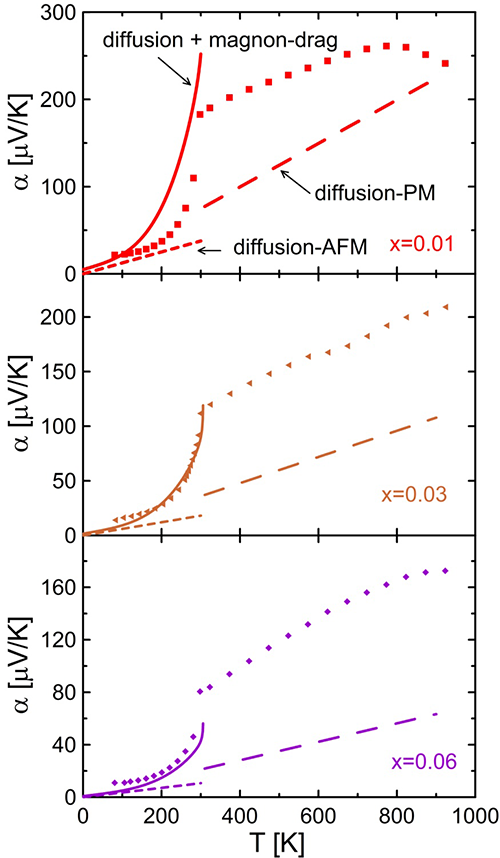图二：Li掺杂样品Mn0.99Li0.01Te、Mn0.97Li0.03Te、Mn0.94Li0.06Te的温度Seeebeck系数曲线，理论计算值与测量值吻合。在低温渐进至尼尔温度TN=310K处磁振子有明显贡献，对应于此处的磁拖曳热电势αMD。测量温度范围中，发现材料同时存在自由电子扩散αD、声子拖曳、磁拖曳，以及新发现的顺磁拖曳热电势效应Δα（延伸至3×TN）。

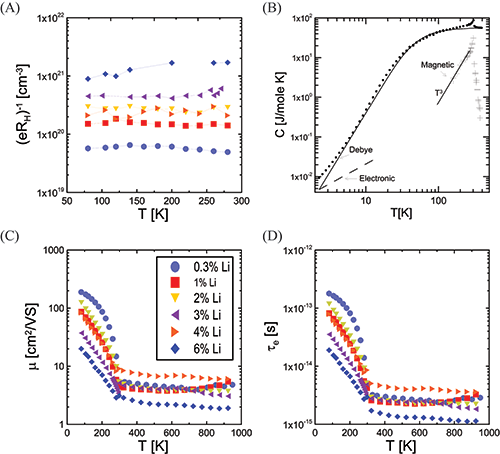图三：通过Hall测量得到的有关样品的变温载流子浓度曲线（A），样品Mn0.94Li0.06Te的比热容分析，黑色圆点显示测量值，低温部分虚线显示电子比热容，在Dulong-Petit高温极限条件下，可利用Debye模型拟合计算出声子比热容，测量数据与声子和电子比热容之和之间的差值即为自旋部分的比热容贡献（B），样品载流子变温迁移率曲线（C），样品载流子寿命变温曲线（D）。

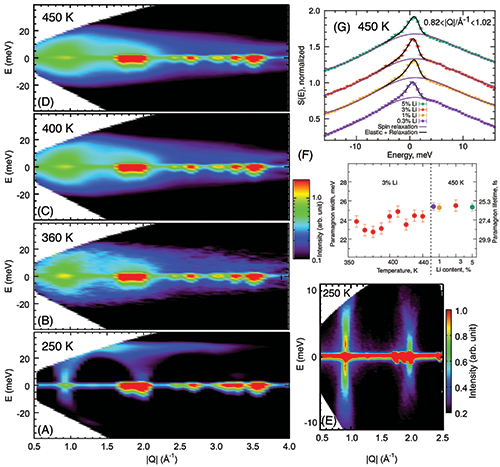图四，非弹性中子散射结果：图(A-D)显示3%Li掺杂MnTe样品的S(Q,E)色散关系，其中(A)对应反铁磁相，(B-D)对应顺磁相。图(E)显示反铁磁相的高分辨S(Q,E)色散关系，发现具有低能散射特征以及一个在Q=0.92Å-1处的约0.6meV的赝能隙存在。图(G)显示系列样品的S(Q,E)色散关系在0.82-1.02Å-1的切面，可见加入弹性模型后与实验数据吻合较好。通过对图(G)数据进行拟合可以得到顺磁磁振子在350-450K之间的能量半高宽和寿命，如图(F)所示。

上述工作得到国家自然科学基金（51572287）和基金委-广东联合重点基金（U1601213）的支持。

参考连接：
[1] .Y. Zheng, T. Lu, Md M. H. Polash, M. Rasoulianboroujeni, N. Liu, M. E. Manley, Y. Deng, P. J. Sun, X. L. Chen, R. P. Hermann, D. Vashaee, J. P. Heremans, H. Zhao., Sci. Adv. 2019; 5: eaat9461
[2]. S. Mu, R. P. Hermann, S. Gorsse, H. Zhao, M. E. Manley, R. S. Fishman, L Lindsay., Phy. Rev. Materials 3，039901（2019）