近年来，非厄米趋肤效应已成为非厄米领域研究的核心问题。非厄米趋肤效应是指大量体本征模式在开放边界条件下局域在低维边界上的现象。这种反常的波函数局域行为与许多物理现象密切相关。例如，在一维体系中，具有趋肤效应的系统表现出非互易的响应性质，对杂质免疫的单向输运等。因此，研究非厄米趋肤效应对于非厄米能带理论的发展至关重要。

　　随着广义布洛赫能带理论的发展，一维趋肤效应可以被很好地描述。然而，维度的增加使得趋肤效应的表现形式变得更加复杂。一个典型的例子是高维体系中的几何依赖趋肤效应，即波函数的局域行为依赖于晶格的开边界几何形状。如何理解和探测这种新型的高维趋肤效应仍是一个尚未解决的问题。

　　此外，尽管人们已经提出了在一维和高维下出现趋肤效应的布洛赫能谱判据（简称“能谱判据”），但在实际的凝聚态系统中，一方面，人们很难在实验中直接探测复能谱在复平面中的位置与结构，因此虽然能谱判据在理论上是很直接的，但却很难被直接应用到实验中；另一方面，由于系统的响应和输运性质往往只取决于费米能附近的特性，因此可能的情况是，根据能谱判据，系统被认为具有趋肤效应，但在特定频率下并不表现出趋肤效应的性质。这意味着我们需要建立更精细的体边对应关系，以确定在给定频率处是否存在波函数的反常局域。

　　最近，中国科学院物理研究所/北京凝聚态物理国家研究中心凝聚态理论与材料计算重点实验室T03组的方辰研究员和其博士研究生张锴（现为美国密歇根大学博士后）与厦门大学杨哲森副教授合作，在非厄米系统中提出了动力学简并劈裂 (dynamical degeneracy splitting) 的概念来表征趋肤效应，揭示了格林函数在给定频率下的一系列反常物理性质。该项工作基于他们之前建立的关于非厄米趋肤效应在一维【延伸阅读：高维体系中的普适非厄米趋肤效应】和高维【延伸阅读：高维体系中的普适非厄米趋肤效应】的理论工作。

　　该研究团队提出的动力学简并劈裂是指对于给定的激发频率，布里渊区中的等频率线 (equal frequency contour) 上不均匀的能量虚部。在给定激发频率下，动力学简并劈裂的发生意味着在此频率下存在趋肤效应，因此建立了依赖频率的体边对应。此外，动力学简并劈裂的发生也意味着格林函数在此频率下的反常，导致了（1）谱函数在动量空间的不均匀展宽，和（2）反常散射。作为应用，他们提出了定向不可见 (directional invisibility) 的波包动力学现象来探测几何依赖趋肤效应。这种现象是指当入射波包撞向某些角度的杂质线时，具有反射波组分，而对于其他角度的杂质线，入射波只有透射没有反射。这项工作可以将趋肤效应的研究推广到更加复杂的自能对频率依赖的凝聚态系统，为非厄米物理的进一步发展奠定了基础。

　　该工作受到中国科学院（XDB33000000）、国家自然科学基金（NSFC-12104450）和博士后创新人才支持计划（BX2021300）等项目的资助。相关研究成果以“Dynamical Degeneracy Splitting and Directional Invisibility in Non-Hermitian Systems”为标题发表在Phys. Rev. Lett. 131, 036402 (2023)，论文链接为https://doi.org/10.1103/PhysRevLett.131.036402。

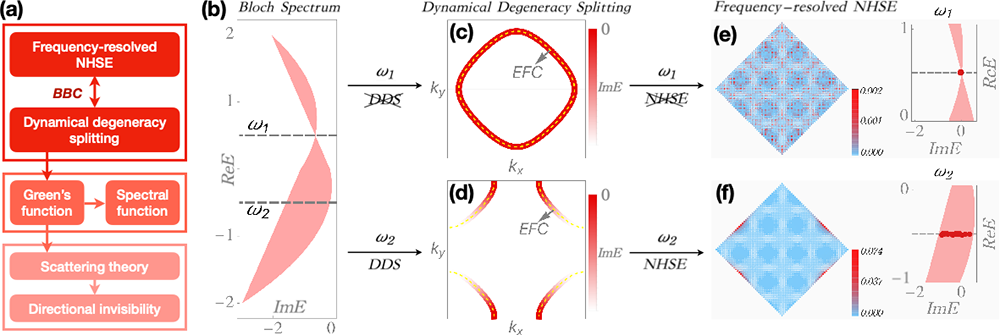
图1：(a) 动力学简并劈裂一方面对应于频率分辨的非厄米趋肤效应；另一方面对应于格林函数，导致了谱函数和散射理论的反常。(b)-(f) 频率依赖的体边对应：在某频率处发生（未发生）动力学简并劈裂，意味着在此频率处存在（不存在）非厄米趋肤效应。

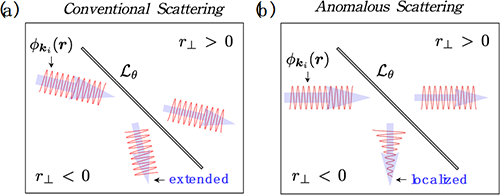
图 2：正常散射 (a) 和反常散射 (b) 的对比示意图。在反常散射中，杂质线将入射平面波散射至衰减的反射波。

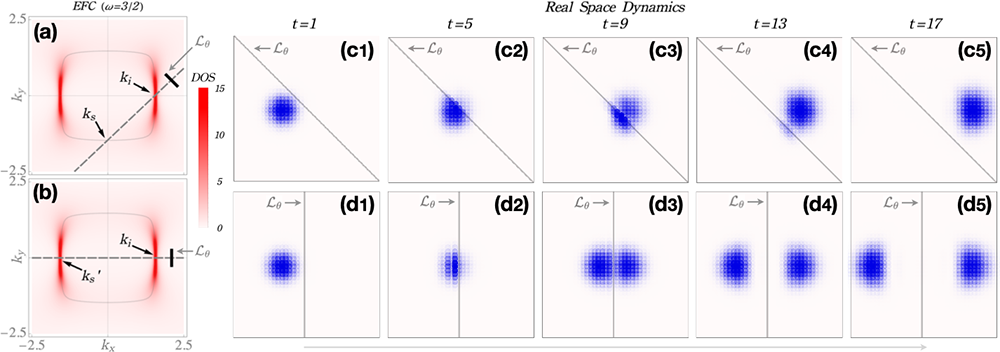
图 3：(a)(b) 当动力学简并发生时，谱函数在等频率线上的分布不均匀。这种情况下，(c1)-(c5) 展示了入射波包能够直接穿过斜向的杂质线，而没有出现可见的反射波组分。相反地，(d1)-(d5) 显示了对于垂直方向的杂质线，入射波包存在明显可见的反射波。这表明了定向不可见的波包动力学现象。