空间上的束缚态是一种限制在一定空间范围内的局域模式，其能量通常位于扩展态的连续谱之外。然而，在某些特殊势阱中，单粒子束缚态的能量会进入连续谱中，这种现象被称为连续谱中的束缚态(bound state in the continuum),简称BIC，是魏格纳和冯·诺依曼于‌1929年首次提出。魏格纳和冯·诺依曼的模型需要精准地逆向设计势函数,这使得连续谱中的束缚态很难在实验上被实现。在上世纪70年代,人们发现连续谱中的束缚态作为一种干涉效应广泛存在于电磁波、声波、水波等经典波动体系。连续谱中的束缚态因其新颖特性和在各种物理系统中的重要应用而引起了广泛关注。尽管大多数关于BIC的研究要聚焦于研究单粒子量子体系中的连续谱中的束缚态, 最近一些理论工作揭示了在多粒子系统中杂质势和相互作用会的共同作用导致连续谱中的多粒子束缚态。这些连续谱中的束缚态通常会局域在杂质势附近。

　　最近，中国科学院物理研究所/北京凝聚态物理国家研究中心凝聚态理论与材料计算重点实验室T01组陈澍研究员和云南大学刘彦霞副教授合作，在非厄米相互作用系统的连续谱中的束缚态性质研究取得了重要进展。

　　由于以往关于BIC的研究大多集中在非相互作用的厄米系统上，非厄米相互作用系统中BIC的形成机制尚不清楚。刘彦霞和陈澍解析地研究了一维相互作用非厄米系统中的BIC，揭示了非互易跃迁项对连续谱中的束缚态命运的影响机制。他们通过具体研究具有广义边界条件或杂质势的非互易两粒子相互作用晶格模型，尽管该模型是不可积的，但通过类似Bethe-ansatz 的方法，他们精确地给出该模型中BIC的波函数和本征值，从而准确绘制出BIC的相图。研究结果显示，非互易跃迁项会导致束缚态不再局域，进而缩减BIC形成区域的范围。通过对波函数的分析，他们发现了两种具有不同空间分布的BIC的存在，并解析地推导出了导致BIC不存在的临界值。他们的解析结果为理解非厄米系统中BIC的命运提供了坚实基础。

　　相关研究成果以题为“Fate of Two-Particle Bound States in the Continuum in Non-Hermitian Systems”的研究论文发表在《物理评论快报》上[Phys. Rev. Lett.133, 193001 （2024）]。陈澍研究员为文章的通讯作者。该工作受到科技部国家重点研发计划 、国家自然科学基金委和中国科学院先导专项等项目的资助。

　　论文链接：https://doi.org/10.1103/PhysRevLett.133.193001

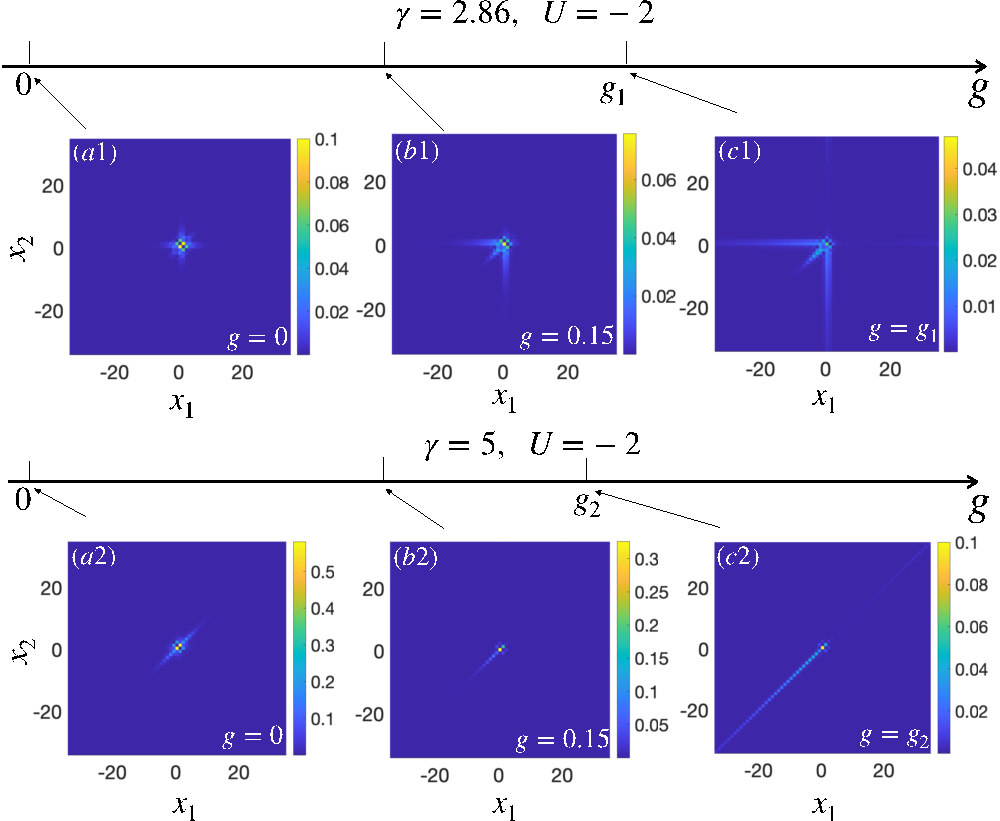
图 两种BIC受非互易跃迁项的影响