中国科学院物理研究所
北京凝聚态物理国家研究中心
T03组供稿
第28期
2016年08月15日
相互作用导致的陈绝缘体在数值模拟中被发现
无相互作用拓扑绝缘体的研究已然汗牛充栋,对于描述这些拓扑物质形态的拓扑不变量,如缠绕数、陈数、Z2不变量等,人们在理论和实验上都了解得比较清楚。相比之下,对于相互作用下拓扑物态的性质和分类,则有太多问题悬而未决。电子相互作用所引入的关联效应,一方面使得体系本身变得复杂,另一方面却往往可以产生更加丰富的物理现象。其中一个比较普遍的思路,就是电子相互作用可以使体系进入非平庸的拓扑物质形态,如相互作用导致的陈绝缘体或者具有拓扑序的自旋液体态。这方面的猜测性研究不少,但是通过定量的数值方法,结合理论分析,确定性的找到相互作用所导致的拓扑物态,这样的研究并不多见。
中国科学院物理研究所/北京凝聚态国家实验室T03组孟子杨副研究员、方辰副研究员,中国人民大学博士研究生邬汉青、何院耀,卢仲毅教授组成的团队(下面简称该团队),在相互作用导致陈绝缘体态的数值计算方面取得了进展[1]。该团队提出了一种针对弱耦合区域相互作用导致的拓扑物态的通用诊断方案。利用严格对角化方法给出的本征值及本征波函数,结合点群操作算符的本征值和关联函数信息,分析出体系热力学极限的序参量对称性和基态可能的拓扑数。根据这一方案,该团队第一次从数值上给出了棋盘格子上具有最近邻排斥相互作用的无自旋费米子模型中存在由相互作用导致陈绝缘体的支持性证据。这个工作最近发表在美国物理学会杂志的Physical Review Letters期刊上。
如图1. (a) 所示,棋盘格子模型哈密顿量具有最近邻跃迁和两种交错排列的次近邻跃迁。在无相互作用时,上下两条能带在布里渊区的M点上有一个二次型的接触点(quadratic band crossing point, QBCP) [图1. (b) 所示]。这个二次型接触点受到C4点群和时间反演的共同保护。如果破坏时间反演并保持C4旋转对称性,例如加入图1. (a) 中绿色箭头所示的环路电流(这类似于在近邻片 (plaquette) 内加入交错磁通,但体系总磁通量保持为零),体系会在M点直接打开单粒子能隙,进入具有非零陈数的陈绝缘体态,系统有整数化的量子霍尔电导和手征边界态。反过来,如果加入保持时间反演但破坏C4对称性的交错在位势能项,那么QBCP就会分裂成两个狄拉克点反向地往X点移动,当狄拉克点在X点相遇时,打开能隙。
在这个模型中加入最近邻排斥相互作用,单圈重整化群分析认为[2],QBCP在相互作用下是不稳定性的,具有手征边缘态。而该研究团队的数值结果确实发现,系统在热力学极限下,在弱相互作用区域就是一种由相互作用诱导自发产生电流环路的陈绝缘体态;该态破坏时间反演,具有手征边界态;而强相互作用区域则是一种电荷重新分布的格点向列序(site-nematic order)绝缘体,该态破坏C4晶体点群对称性。图1. (c) 给出了系统在相互作用下的完整相图。
图2. (a) 展示了系统最低的四个本征能量随相互作用的变化情况。在 Vc / t ≈ 2.8处能级出现交叉。在交叉前,能级具有两重简并,互为时间反演共轭对的两重简并基态波函数构成C4点群二维不可约表示的基函数,对应C4操作的本征值为±i (见表1, V<Vc)。在一个有限尺寸体系和弱相互作用下,能够证明对一个有能隙的系统,其基态波函数所携带的陈数与周期边界条件下一些旋转操作算符的本征值直接相关[3]: iC=ζ, ζ为C4操作算符本征值, C 是陈数。所以这两个简并态分别携带着C=1mod4、C=-1mod4的非零陈数。对于一个有能隙的体系,它的热力学基态的拓扑数(包括陈数)都是唯一的,基态不会是具有不同陈数的多个量子态的线性叠加,因此在逼近热力学极限的过程中,体系必然自发破缺时间反演对称性,选择具有某一确定陈数的基态作为热力学基态,所以模型在弱相互作用的热力学极限下是一个陈绝缘体态。这个绝缘体态也在图2. (b) 的单粒子能隙打开情况得到确认。该团对也计算了环路电流的关联函数所对应的结构因子,如图3. (a) 所示,它在弱相互作用区域具有一个宽峰,表明这种环路电流序在热力学极限下可以稳定存在。综上,可以说明模型在热力学极限下的弱相互作用区域是一个自发形成环路电流破坏时间反演的陈绝缘体。
而在强相互作用区域,有限尺寸体系的两个近简并基态构成C4点群的一维表示。它们所携带的陈数可以通过基态波函数对边界缠绕相位的线性响应计算得到。该团对发现它们的陈数都为零 (见表1,V>Vc),在拓扑上是平庸的态。而它们的C4本征值符号相反,但是C2操作算符的本征值相同。两个相同陈数的态在热力学极限下可以线性组合,那么强相互作用区域的热力学极限态应该是一种破坏C4对称性但保留C2对称性的一种绝缘体态。通过A和B子格电荷密度差的结构因子的计算,该团对确认了这种绝缘体相是破坏C4对称性的格点向列序型绝缘体。
从领域的发展来看,2008年S. Raghu 等人首先给出了蜂巢晶格上可能存在相互作用导致陈绝缘体的理论预言[4]。然而近几年来,这一个猜想受到了不少理论和数值研究的质疑,相互作用导致陈绝缘体并没有被发现。这是因为二维系统的狄拉克点在弱短程电子-电子相互作用下是稳定的,所以无质量的狄拉克费米子能够在一个有限的临界相互作用前存在。超出了弱耦合区域,平均场和单圈重整化群方案的结果是不可靠的,其他可能的长程序与陈绝缘体相强烈竞争。而在工作 [1] 中,相互作用导致陈绝缘体被成功发现,这是因为工作 [1] 研究的模型具有二次型接触的能带,费米面处有有限的态密度,短程相互作用是略微相关的,而且QBCP的动态临界因子z=2,也就是QBCP点处低能有效维度为d+z=4。根据朗道-金兹堡判据,平均场分析结果是可靠的,该团队的严格对角化数值结果和点群操作算符的本征值和关联函数信息的分析,成功地确认了相互作用导致陈绝缘体,推动了相互作用拓扑物态领域继续向前发展。此外,该团队发展的数值诊断方案(严格对角化数和点群操作算符的本征值分析)是通用的,可以推广到其他体系的弱耦合区域相互作用导致的拓扑量子物态 (例如量子自旋霍尔绝缘体,p+ip超导等) 的探测中。
这项工作得到了科技部国家重点研发计划(方辰、孟子杨),国家自然科学基金和国家基础科学研究计划(邬汉青、何院耀、孟子杨、卢仲毅)的支持。严格对角化方法所需的并行计算在中国人民大学物理系高性能并行计算物理实验室,中国科学院物理研究所量子科学模拟中心,国家超级计算广州中心天河2号等计算平台上完成。
[1] H. -Q. Wu, Y. -Y. He, C. Fang, Z. Y. Meng and Z. –Y. Lu, Phys. Rev. Lett. 117, 066403 (2016).
[2] K. Sun, H. Yao, E. Fradkin, and S. A. Kivelson, Phys. Rev. Lett. 103, 046811 (2009).
[3] C. Fang, M. J. Gilbert, and B. A. Bernevig, Phys. Rev. B 86, 115112 (2012).
[4] S. Raghu, X.-L. Qi, C. Honerkamp, and S.-C. Zhang, Phys. Rev. Lett. 100, 156401 (2008).
中国科学院物理研究所/北京凝聚态国家实验室T03组孟子杨副研究员、方辰副研究员,中国人民大学博士研究生邬汉青、何院耀,卢仲毅教授组成的团队(下面简称该团队),在相互作用导致陈绝缘体态的数值计算方面取得了进展[1]。该团队提出了一种针对弱耦合区域相互作用导致的拓扑物态的通用诊断方案。利用严格对角化方法给出的本征值及本征波函数,结合点群操作算符的本征值和关联函数信息,分析出体系热力学极限的序参量对称性和基态可能的拓扑数。根据这一方案,该团队第一次从数值上给出了棋盘格子上具有最近邻排斥相互作用的无自旋费米子模型中存在由相互作用导致陈绝缘体的支持性证据。这个工作最近发表在美国物理学会杂志的Physical Review Letters期刊上。
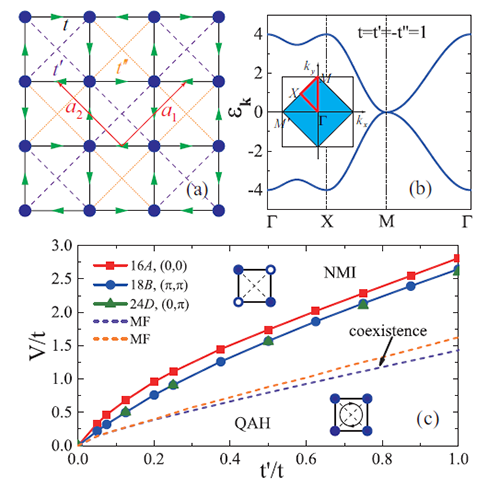 |
| 图1. (a) 具有C4对称性的16个格点的棋盘格子。a1和a2为原胞基矢,t, t', t'' 为最近临和次近邻跃迁。(b) 无相互作用模型的能带图。二维情况下的二次型接触点贡献出有限的态密度。(c) 棋盘格子上相互作用模型的基态相图, V 是相互作用参数。 |
在这个模型中加入最近邻排斥相互作用,单圈重整化群分析认为[2],QBCP在相互作用下是不稳定性的,具有手征边缘态。而该研究团队的数值结果确实发现,系统在热力学极限下,在弱相互作用区域就是一种由相互作用诱导自发产生电流环路的陈绝缘体态;该态破坏时间反演,具有手征边界态;而强相互作用区域则是一种电荷重新分布的格点向列序(site-nematic order)绝缘体,该态破坏C4晶体点群对称性。图1. (c) 给出了系统在相互作用下的完整相图。
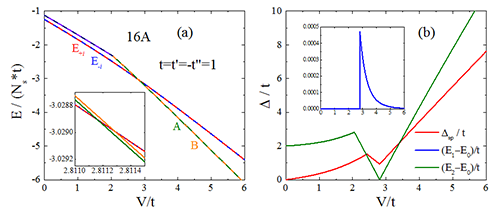 |
| 图2. (a) 严格对角化方法计算的16个格点模型的最低的四个本征能量随相互作用改变情况,(b) 单粒子能隙和多体能隙随相互作用的变化。 |
 |
| 表1. 16个格点有限团簇计算的多体本征态的对称性质。SSB表示自发对称性破缺。 |
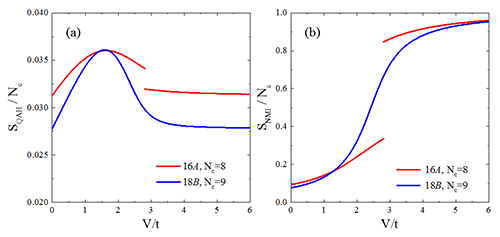 |
| 图3. 环路电流结构因子 (a) 和格点向列序结构因子 (b) 随着相互作用和系统尺寸的变化情况。 |
这项工作得到了科技部国家重点研发计划(方辰、孟子杨),国家自然科学基金和国家基础科学研究计划(邬汉青、何院耀、孟子杨、卢仲毅)的支持。严格对角化方法所需的并行计算在中国人民大学物理系高性能并行计算物理实验室,中国科学院物理研究所量子科学模拟中心,国家超级计算广州中心天河2号等计算平台上完成。
[1] H. -Q. Wu, Y. -Y. He, C. Fang, Z. Y. Meng and Z. –Y. Lu, Phys. Rev. Lett. 117, 066403 (2016).
[2] K. Sun, H. Yao, E. Fradkin, and S. A. Kivelson, Phys. Rev. Lett. 103, 046811 (2009).
[3] C. Fang, M. J. Gilbert, and B. A. Bernevig, Phys. Rev. B 86, 115112 (2012).
[4] S. Raghu, X.-L. Qi, C. Honerkamp, and S.-C. Zhang, Phys. Rev. Lett. 100, 156401 (2008).

