传统计算系统,从材料、器件到电路、架构再到容错系统和算法设计,都在竭力避免随机性。然而,随着后摩尔时代的来临以及学界对非冯诺依曼架构兴趣的提升,人们越来越倾向于在计算架构中拥抱随机性而非本能地排斥之,特别是在天然具有随机性特征的计算中,如蒙特卡罗抽样、贝叶斯神经网络、贝叶斯推理网络、模拟/量子退火算法加速器,乃至新兴的生成式人工智能等等。
引入随机性时,两点非常重要:随机数的质量和分布。前者需要通过物理熵源——物理过程的本征随机性来保证而后者——概率分布函数(Probabilistic Distribution Function, PDF)决定了概率计算算法的成败。尽管经典计算机可在软件层面引入特定PDF的伪随机数,如累积分布函数(CDF)的反函数方法和接受-拒绝抽样方法等,但是这种软件层面的随机数生成方式显然耗时低效。为应对PDF要求严格、随机数吞吐量较大、速度能耗要求较高的应用场景,开发PDF可调的硬件级真随机数生成器(TRNG)成为一种必然选择。磁性隧道结(Magnetic Tunnel Junction, MTJ),当其磁结构被预置到磁翻转的临界状态时,因受热激活过程的扰动,它的电阻值可在高低阻态——反平行和平行的磁结构之间随机跳变;并且,系统状态距离临界状态的程度,可受外界触发条件(如电流、电压、温度等)精确控制,即MTJ电阻随机跳变的概率可受上述条件连续控制。因此这一过程成为开发可调概率TRNG的理想物理熵源。
中国科学院物理研究所/北京凝聚态物理国家研究中心磁学室M02课题组开发了高性能自旋轨道转矩(Spin-orbit Torque, SOT)驱动型MTJ,其尺寸为50nm×200nm,写入速度为300ps,室温下隧道磁阻比超过100%,并具有超过1012次的实测循环写入耐用性。更有意思的是这类SOT-MTJ的翻转概率受驱动电压连续调控,使其成为一种概率从0%到100%连续可调的0或1二元TRNG——伯努利TRNG。它以可调的概率p或(1-p)抽样出高阻态(1)或低阻态(0)。
更进一步,他们还开发了从二元伯努利TRNG向应用场景更广泛的(准)连续型TRNG扩展的高效算法。任何一个自然数,都可以分解成诸如10110…的二进制字符串,如0-15之间的自然数N可以写成4位字符串ABCD,其中A-D是二元随机变量。因此预使得自然数N满足概率分布函数p(N),实际上只需要寻找到二元随机变量A-D之间恰当的相互制约或因果关系。而后者刚好可以通过贝叶斯网络——一种非常适合编码因果关系的随机神经网络来描述。借助贝叶斯网络这一强大工具,M02课题组导出了将p(N)关系转译成贝叶斯网络参数的算法。随后利用SOT-MTJ——二元TRNG作为网络节点,利用p(N)转译的网络联接权重,借助由此生成的四节点贝叶斯推理网络(ABCD),他们巧妙地实现了可配置概率分布函数(包括均匀分布、高斯分布、指数分布、卡方分布即其他自定义分布)的TRNG,这不仅能满足随机计算、概率计算、模拟退火、模拟量子退火、蒙特卡洛模拟、数字孪生等等应用场景的需求,更能在生成式人工智能时代释放自旋电子熵源器件的巨大潜力,极大地拓展SOT-MTJ器件的适用范围。
该工作已在《Advanced Science》刊发。中国科学院物理研究所M02课题组韩秀峰研究员、万蔡华副研究员为论文共同通讯作者构思和指导了该项研发;中国科学院物理所博士生张然是该论文第一作者。其他合作者参与了器件制备、测试、数据分析和论文写作。该工作致谢科技部重点研发项目和基金委重点基金等项目经费支持。https://doi.org/10.1002/advs.202402182.
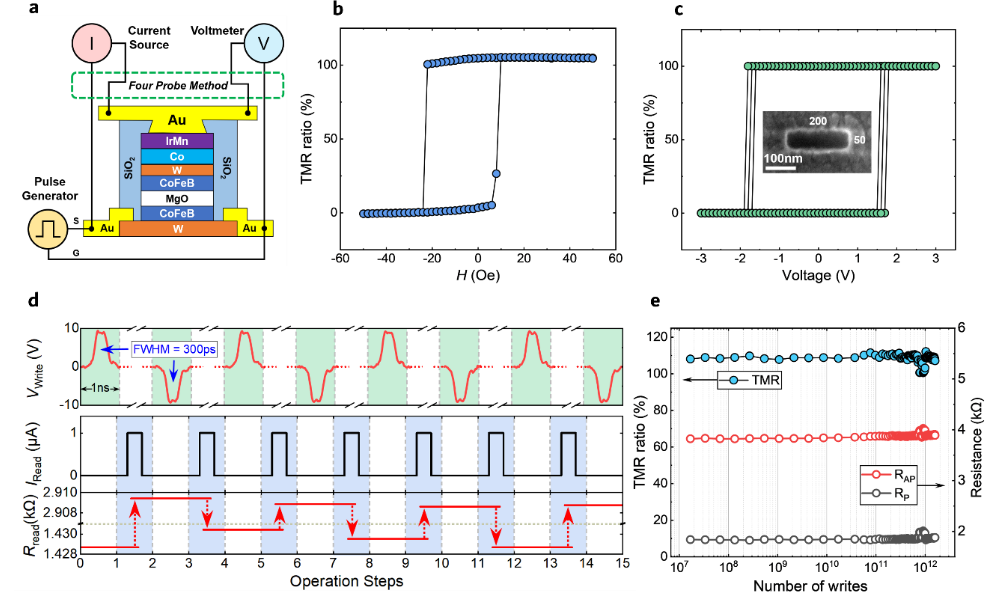
图 1. 自旋轨道力矩磁性隧道结(SOT-MTJ)零场电流驱动的翻转性能表征。(a)器件结构和测量示意图。(b)通过沿MTJ易轴扫描面内磁场获得的R-H回线。(c)由脉冲电流驱动的零场磁化翻转。插图是MTJ的扫描电子显微镜(SEM)顶视图。(d)由300ps脉冲驱动的零场磁化翻转。(e)在2.4倍临界写入电压下进行的超过1012次写入耐久性测试。

图 2. 基于MTJ的可调真随机数生成器(TRNG)的实验演示。(a)基于MTJ的TRNG的几种不同实现。(b)MTJ翻转概率与写入电压的关系。黑色实线为拟合的S型曲线。(c-e)在特定电压0.8V(c)、0.9V(d)和1.0V(e)下连续测试得到的电阻结果。
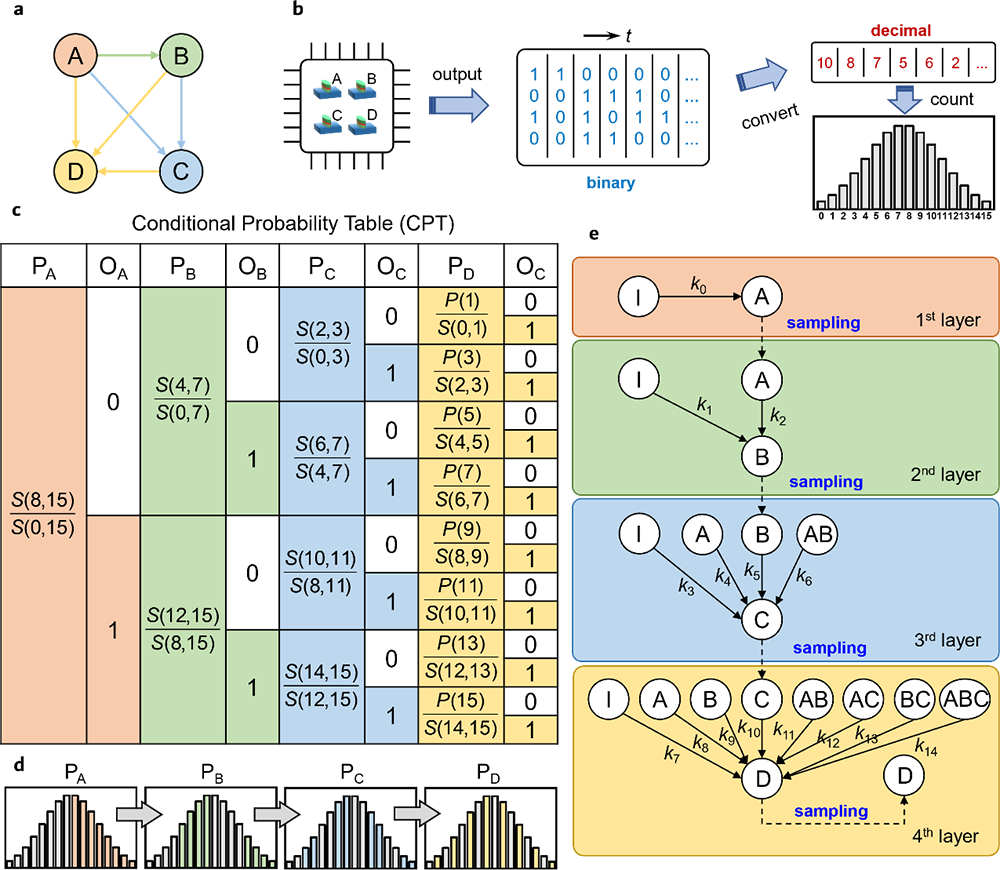
图 3. 提出的可调PDF的真随机数生成器示意图。(a)用于生成随机数N的贝叶斯网络。(b) 生成具有所需PDF的随机数的过程。(c)随机数生成器使用的条件概率表(CPT)。此处S(i,j)=ΣijP(N)。(d)中的条件概率与所需分布概率之间的关系。e)根据设计的PDF生成真随机数的网络。它包含4层,每层通过虚线指示采样随机数的一个比特A、B、C和D。
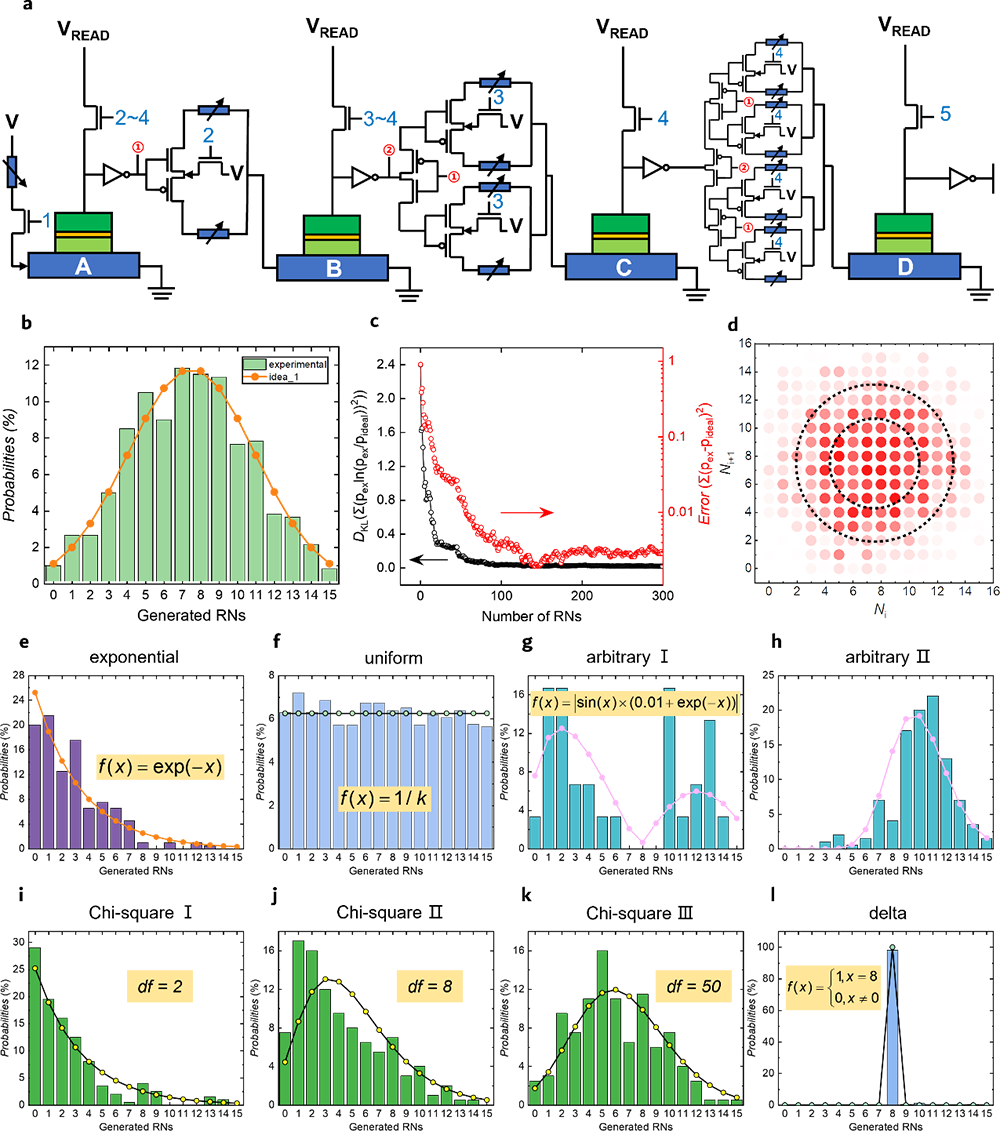
图 4. 基于SOT-MTJ的PDF可调TRNG的采样结果。(a)用于级联采样伯努利比特A、B、C和D的电路实现方案。(b)高斯PDF的实现。(c)随着生成随机数数量的增加,测量的PDF与所需PDF之间的偏差。(d)生成的相邻随机数Ni和Ni+1之间没有相关性。(e-h)指数PDF、均匀分布和两个任意定义的PDF。(i-k)具有不同参数df = 2、8和50的卡方PDF。(l)单峰型PDF,意味着TRNG可以几乎100%的概率选择性地输出0~15之间的任何数字。

