凝聚态物理体系中磁场驱动导致的几类量子振荡现象大都非常优美，它们的出现都与一些特定的物理机制有关。例如，在超导环的Little-Parks实验中可观测到超导转变温度（T_c）随磁场（B）的周期性振荡；在介观导体环中出现以B为振荡周期的Aharonov-Bohm和Altshuler-Aronov-Spivak振荡。上述两种量子振荡都涉及磁通量子化现象。再如，在de Haas–van Alphen (dHvA) 和 Shubnikov–de Haas (SdH)效应中，一些可观测物理量表现出以1/B为周期的振荡，其物理机制源于磁场中电子轨道的朗道量子化。近来在个别体系中还报道有随对数磁场的电阻振荡等。

　　最近，中国科学院物理研究所/北京凝聚态物理国家研究中心固态量子信息与计算实验室Q02/HX-Q02组屈凡明研究员、吕力研究员团队与T06组周毅研究员团队、HM-01组石友国研究员团队、电子科技大学刘富才教授团队等合作，在基于电荷密度波(TaSe₄)₂I和TaS₃一维纳米线中发现了一种新型的电驱动型量子振荡现象，即电压V随着电流倒数1/I呈现出周期性的振荡。从现象上看，这种以1/I为周期的振荡与以1/B为周期的dHvA、SdH磁驱动量子振荡有异曲同工之妙。

　　(TaSe₄)₂I和TaS₃是一种拥有范德瓦尔斯结构的准一维电荷密度波材料，研究团队利用胶带解离方法得到其纳米线，利用Ti/NbTiN或Ti/Nb材料制备电极，并分析其伏安特性（V-I）曲线随温度的变化。在温度从室温经过电荷密度波转变温度T_CDW降到系统基温1.55K过程中，V-I曲线渐渐表现出非线性行为，并在一定电流区间内微分电阻接近于零，表明理想Fröhlich电导态的出现（微分电导趋于无穷大）。有意思的是，在Fröhlich电导区域，V随I表现出锯齿型振荡。如果将横坐标轴转换为1/I，则表现为周期性振荡（图1、3、4），并且振荡指数n可以到1（图3）。这种振荡现象在不同器件和不同电荷密度波材料中都能重复。通过对大量器件的测量，研究团队认为它的出现需要满足特定的条件，包括但不限于：电极与材料界面有较低的耗散、较低的电磁噪声干扰、纯净的电荷密度波电流（滑移之前绝缘性好）、远低于T_CDW的温度等（图2、4）。

　　周毅研究员的初步理论模型认为在电荷密度波绝缘体中，电流驱动其滑移，可等效于存在一个时间周期势，能够产生Floquet子能带（图4）。以这些子能带作为媒介，一端电极处的电子通过共振隧穿（相干输运）的形式进入另一端电极，故当电极费米面与电荷密度波纳米线中某子能带对齐时，对应于V-I曲线中的电压骤降，即电压振荡。在这个前提下，该模型同时巧妙地给出了以1/I为周期的振荡规律，与实现结果吻合。

　　相关研究成果以“Inverse-current quantum electro-oscillations in a charge density wave insulator”为题发表在Physical Review B上。中国科学院物理研究所Q02/HX-Q02组博士后乐天（已出站）和博士生蒋睿阳为共同第一作者，屈凡明研究员和吕力研究员为共同通讯作者；合作者还包括吕昭征副研究员、沈洁特聘研究员、刘广同研究员、李治林副研究员、南开大学曹学伟教授等。上述工作得到国家重点研发计划项目、国家自然科学基金委、中国科学院先导专项、科技创新2030―“量子通信与量子计算机”重大项目、综合极端条件实验装置等的资助。

　　相关工作链接：

　　https://doi.org/10.1103/PhysRevB.109.245123

图1.a.(TaSe₄)₂I纳米线器件D2的V-I曲线随温度的变化；b.在1.55K电压V随电流I变化呈现的锯齿型振荡；c.电压V随电流倒数1/I的变化。

图2.a.(TaSe₄)₂I纳米线器件D3的V-I曲线中振荡随温度的变化，当温度高于NbTiN的超导转变T_c时，振荡曲线开始变得模糊；b.8K时V-I曲线中的振荡随磁场的变化，当外加磁场高于NbTiN的上临界场H_c2时，振荡曲线开始变得模糊；c.1.55K时V-I曲线中的振荡随磁场的变化；d.Ti/NbTiN电极的R-T曲线随磁场的变化。 

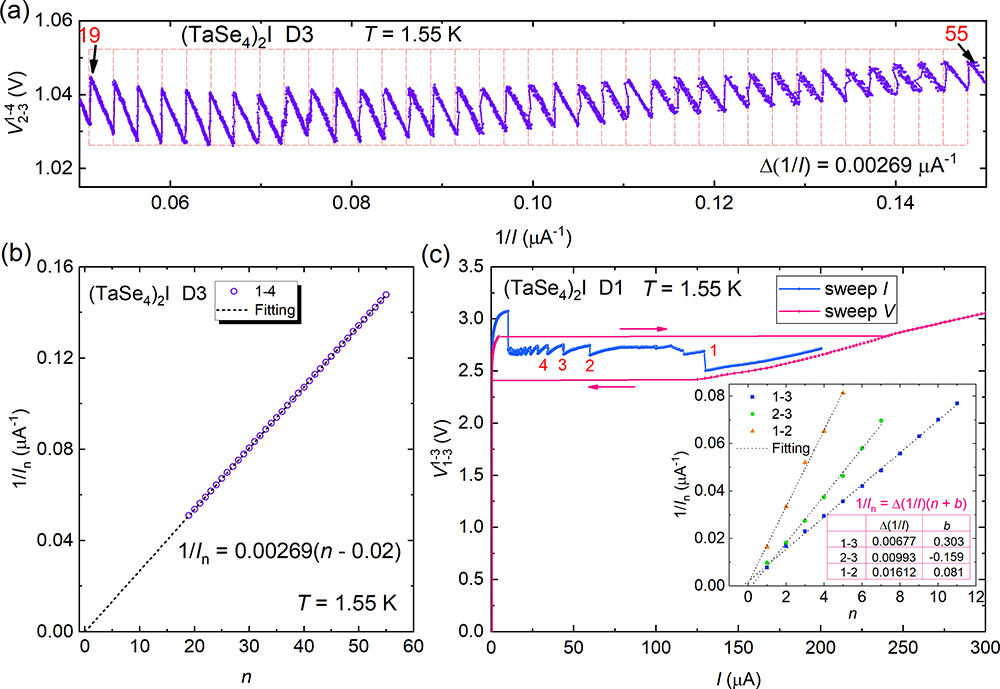
图3.a.(TaSe₄)₂I纳米线器件D3中V随1/I的变化，表现出完美的周期性；b.D3的V-I曲线中每个振荡位置的1/I_n随振荡指数n表现出的线性行为；c.在D1器件中观测到振荡指数n可以达到1，之后随着电流增加振荡消失。  

图4.a.在测量线路中加滤波后可以使振荡表现地更加明显；b和c.在TaS₃纳米线器件中观测到的1/I周期的振荡；d.滑移电荷密度波态中以Floquet子能带为媒介的共振隧穿模型。