非厄米体系在过去几年受到理论和实验学家的广泛关注,其相关物理性质的研究仍在蓬勃发展。较于厄米哈密顿量描述的体系,非厄米系统拥有例外点/线(Exceptional point/line)、趋肤效应等独有特征。其中例外点是一种与Dirac点和Weyl点完全不同的能级简并点。在例外点处,简并的本征能量一般呈现分数型色散关系且对应的本征波函数合并(coalescence)。非厄米例外点在很多有趣的现象或功能应用中起着关键作用,如单向传输/反射、单模激光和传感增强等,并已在光学、声学、冷原子、量子随机行走、电路等各种平台上实现。
例外点根据其附近的简并能级个数可定义其阶数。例外点附近的能谱一般在参数空间呈黎曼面结构。尽管之前大量的研究已展示了例外点带来的丰富物理性质,然而关于各种不同阶数例外点(以及由其扩展成的例外线)的一个基本问题-拓扑分类仍未解决;另外,如何系统性地构造具有不同拓扑性质的例外点也没有统一的方法。进一步,当体系存在多个例外点/线时它们之间的相互影响也并不清楚。至今仍未建立一个有效理论框架来分析多个例外点/线共同产生的“集体行为”以及新的物理效应。
最近,中国科学院物理研究所/北京凝聚态物理国家研究中心凝聚态理论与材料计算重点实验室T01组胡海平特聘研究员、博士后郭翠仙、陈澍研究员,以及复旦大学丁鲲教授合作提出了普适的具有多个例外点/线非厄米多带体系满足的非阿贝尔守恒规则(non-Abelian conservation rule)。该项工作建立了描述含多个例外点/线的非厄米体系的理论分析框架,并揭示体系的集体行为由辫子群拓扑不变量决定。该项工作基于他们之前建立的关于非厄米能带拓扑分类【Knots and Non-Hermitian Bloch Bands, Phys. Rev. Lett.126, 010401 (2021)】以及关于单个例外点/线拓扑分类 【Knot topology of exceptional point and non-Hermitian no-go theorem, Phys. Rev. Res.4, L022064 (2022)】的同伦群理论。该研究团队进一步发现一般的含多个例外点/线的多带体系存在的一些违反直觉的现象。例如(1)两个具有成对产生的(具有相反拓扑荷)的例外点,当它们再次相遇时不一定湮灭,而是依赖于其相互靠近的路径且呈现出一种“近邻”效应。(2)不对易的例外线由于受到非阿贝尔守恒规则的严格限制,某些构型是禁戒的,如常见的Holf link是不允许的。此外,该研究团队还提出了在声学腔等实验平台上实现和观测这些非阿贝尔拓扑现象的方案。这项研究不仅让人们更全面地理解多带非厄米系统中的非阿贝尔行为,而且可为声学、光学、冷原子等非守恒系统中开展进一步的理论和实验工作提供了新的思路。
相关研究成果发表在Phys. Rev. Lett. 130, 157201 (2023)。
论文链接https://doi.org/10.1103/PhysRevLett.130.157201。
该工作受到科技部国家重点研发计划 (2022YFA1405800) 、国家自然科学基金委 (No. 11974413, No. T2121001) 和中国科学院 (No. XDB33000000) 及启动基金等项目的资助。

图1:一般参数空间中的非阿贝尔守恒规则。(a)黑点代表初时 t=ti 例外点的位置,随着时间演化例外点在参数空间中移动,红色空心点代表其末时 t=tf 位置。对于如图所示路径 Γ,守恒规则指出,只要在演化过程中没有例外点逃逸或进入该路径,则初时和末时沿着该路径的非阿贝尔拓扑不变量共轭:bΓ (t=ti)~bΓ (t=tf)。(b)非阿贝尔拓扑不变量可理解为能级沿着路径的编织,对于 N 带体系,该编织由辫子群 BN 的某个群元描述。
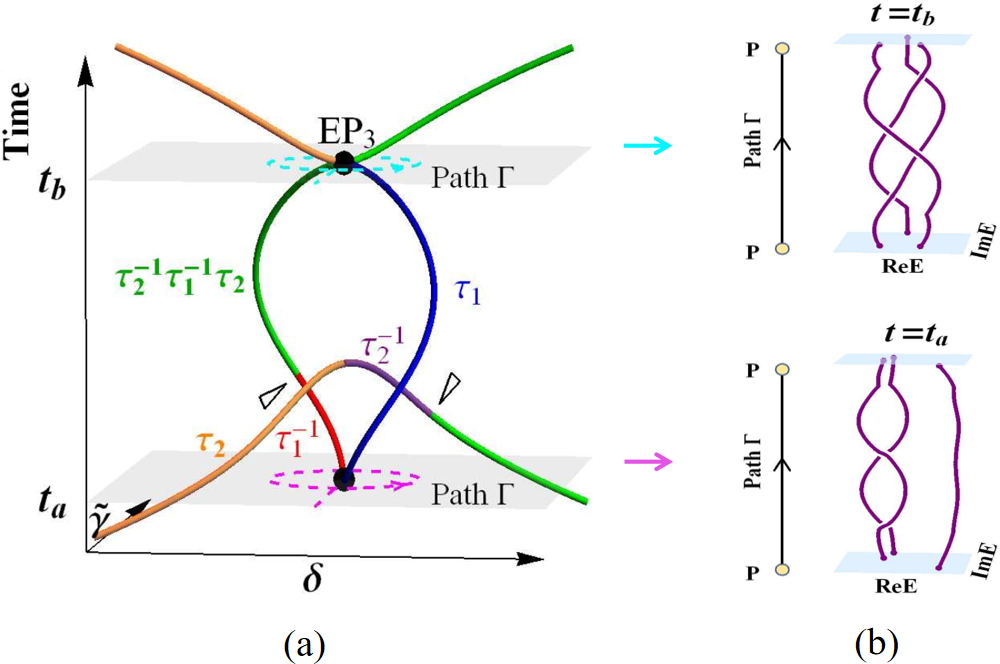
图2:(a) 随着时间演化,例外点在参数空间 \((\delta, \tilde{\gamma})\) 中形成的轨迹,不同颜色代表具有不同的辫子群不变量的例外点。在 t=ta 时成对产生的例外点(下面黑色圆点处),当它们于 t=tb 时再次相遇时,不会湮灭,而是融合成一个三阶例外点(上面黑色圆点处)。(b) t=ta 以及 t=tb 时,沿着路径 Γ 的能级编织图。 t=ta 时,能级编织为平庸的,即bΓ (ta)=1,对应于两个例外点可相互湮灭,t=tb 时,能级编织为非平庸,\(b{_\mit{\Gamma}}\left(t_b\right)=\tau_1 \tau_2^{-1} \tau_1^{-1} \tau_2\),对应于两个例外点不可相互湮灭。

图3:由于受到非阿贝尔守恒规则的约束,不对易的例外线(红色和蓝色)形成的构型会受到严格限制。(a) Hopf link构型为禁戒的构型;(b) 一种守恒规则允许的交错环构型。

