单质铁的结构与磁性在高温下会发生显著的变化。低温相α铁具有体心立方晶格，在居里温度1043 K以下表现为铁磁性；随温度上升存在两种顺磁态下的结构相变，即在1185 K转变为面心立方γ相和在1667 K转变为体心立方δ相。尽管α相的基态行为可以由铁磁Stoner理论来描述，其在高温下转变到γ和δ相的物理机制还没有得到广泛认可的解释。早期的理论研究由于只单独考虑磁自由度或振动自由度，在铁的高温相变是磁熵还是振动熵占主导这一问题上存在很多争论。近年来实验上对铁在不同相变点附近声子谱的非弹性中子散射研究表明：α-γ相变是由同等的振动熵和磁熵的增加导致，而γ-δ变主要源于振动熵的增加。这些实验进展阐明了高温γ和δ相的热力学稳定机制，但其背后的物理作用机制仍有待深入研究。在准简谐近似下，人们利用动力学平均场理论等方法，通过引入有限温度的磁相互作用较好解释了铁在α-γ相变点的声子色散行为，但在γ-δ相变点得到的结果与实验偏离很大。
　　对于大多数金属，晶格的非谐效应即声子-声子相互作用在高温下变得尤为重要。这一点已在三族元素（Sc，Y，La）和四族元素（Ti，Zr，Hf）的研究中被证实。最近，中国科学院物理研究所/北京凝聚态物理国家实验室（筹）凝聚态理论和材料计算研究室T02组博士研究生廉朝胜、王建涛研究员与美国内华达大学的陈长风教授合作，通过结合自洽的第一性晶格动力学方法与反铁磁近似下的有效磁力方法研究了铁在γ-δ相变点附近的声子色散行为。他们的计算结果表明：在高温δ相中，非谐的声子-声子相互作用会引起显著的声子重整化，从而保证其开放体心立方晶格的动力学稳定性；相反，在密排面心立方γ相中，这种非谐效应很弱，其动力学稳定性主要源于磁相互作用（图一）。进一步, 他们从与非磁近似下的结果对比中认识到，在顺磁铁中电子的磁性与晶格自由度相互耦合，单独考虑其中一个自由度并不能正确地描述其在高温下的晶格动力学行为。在同时考虑非谐声子-声子相互作用和磁相互作用的情况下，他们计算得到的高温γ和δ铁的声子谱以及从这些声子谱拟合得到的弹性常数与最近的实验结果非常一致。这一工作突出了晶格的非谐效应在铁的高温相稳定性中扮演的关键角色，并将对其它高温顺磁金属如Ce和Pu的进一步研究有重要的借鉴意义。相关研究结果发表在2015年11月24日出版的Physical Review B 92,184110 (2015)上。
　　该工作得到了国家自然科学基金委和中国科学院的支持。
相关工作链接：
1.Ab initio study of the anharmonic lattice dynamics of iron at the g-d phase transition
http://journals.aps.org/prb/abstract/10.1103/PhysRevB.92.184110

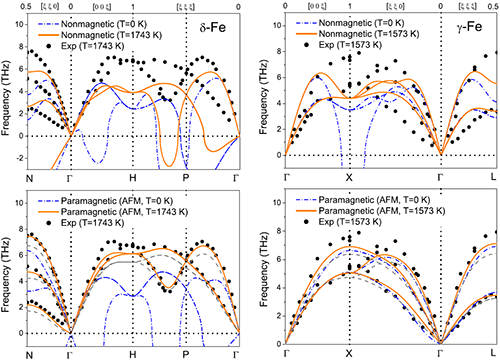图一：顺磁bcc δ-Fe（左）和fcc γ-Fe（右）的声子谱。其中黄色实线是高温自洽声子计算的结果，黑色圆点是非弹性中子散射实验数据。